정리) 하이퍼볼릭 탄젠트 함수는 로지스틱 함수에 비해 출력 범위가 2배로 넓어서 역전파 알고리즘의 수렴에 효과적이다.
하이퍼볼릭 탄젠트 함수(hyperbolic tangent, tanh)
스케일이 조정된 로지스틱 함수
로지스틱 함수에 비해 하이퍼 볼릭 탄젠트 함수는 출력 범위를 (-1, 1)로 넓혀서 역전파 알고리즘의 수렴을 향상시킬 수 있다.
하이퍼볼릭 탄젠트 함수는 logistic(2Z)X2-1과 같다.
import matplotlib.pyplot as plt
def tanh(z):
e_p=np.exp(z)
e_m=np.exp(-z)
return (e_p-e_m)/(e_p+e_m)
z=np.arange(-5, 5, 0.005)
log_act=logistic(z)
tanh_act=tanh(z)
plt.ylim([-1.5, 1.5])
plt.xlabel('Net input $z$')
plt.ylabel('Activation $\phi(z)$')
plt.axhline(1, color='black', linestyle=':')
plt.axhline(0.5, color='black', linestyle=':')
plt.axhline(0, color='black', linestyle=':')
plt.axhline(-0.5, color='black', linestyle=':')
plt.axhline(-1, color='black', linestyle=':')
plt.plot(z, tanh_act, linewidth=3, label='Tanh')
plt.plot(z, log_act, linewidth=3, label='Logistic')
plt.legend(loc='lower right')
plt.tight_layout()
plt.show()
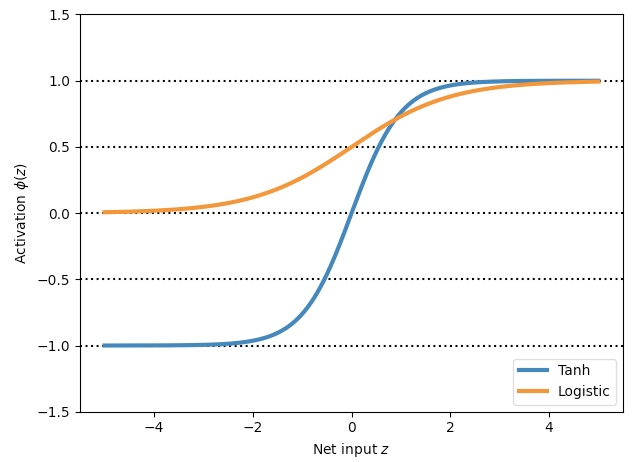
tanh 함수가 logistic 함수보다 2배 큰 출력 범위를 가진다.
넘파이 & 텐서플로의 하이퍼탄젠트 함수( tf.keras.activations.tanh() )
np.tanh(z)
array([-0.9999092 , -0.99990829, -0.99990737, ..., 0.99990644,
0.99990737, 0.99990829])
tf.keras.activations.tanh(z)
<tf.Tensor: shape=(2000,), dtype=float64, numpy=
array([-0.9999092 , -0.99990829, -0.99990737, ..., 0.99990644,
0.99990737, 0.99990829])>
텐서플로의 시그모이드 함수
tf.keras.activations.sigmoid(z)
<tf.Tensor: shape=(2000,), dtype=float64, numpy=
array([0.00669285, 0.00672617, 0.00675966, ..., 0.99320669, 0.99324034,
0.99327383])>